252DREICKE
„252 Dreiecke“ ist ein Projekt, das sich mit der Veränderung von Formen und der Manipulation eines immer gleich großen Kreises und seiner Achtel in Form von Dreiecken befasst.
Inspiriert wurde das Projekt durch die genauere Betrachtung der Abwicklung von Blüten, bei der sich herausstellte, dass diese in der Regel einen groben Kreis darstellen. Dabei sind die Abschnitte oft gleichmäßig aufgeteilt, zum Beispiel in Drittel, Viertel, Sechstel oder Achtel.
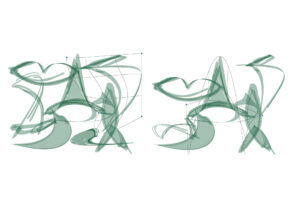
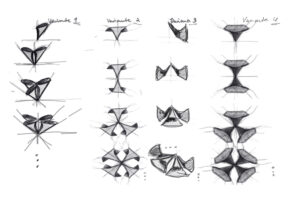
Die Formstudie von „252 Dreiecke“ dokumentiert die Veränderung eines immer gleich großen Achtels eines Kreises in sechs verschiedenen Formen. Der Kreis mit einem Durchmesser von 27 cm wird in acht gleich große Dreiecke unterteilt, hierbei wird jedes Achtel anders verformt. Ziel des Projekts war es zu erforschen, welche dreidimensionalen Formen aus derselben Fläche möglich sind zu konstruieren und wie sich das Volumen verändert, wenn mehr verformte Achtel hinzugefügt werden.
Für das Projekt wurde Draht für eine einfache Verformung und Moosgummi als Hauptmaterial benutzt.
Während des Experiments wurde mit Hilfe der Manipulation dieser bestimmten Dreiecke festgestellt, dass jede dreidimensionale Form unterschiedliche Volumenveränderungen aufweist. Manche der verformten Kreise schließen oder öffnen sich, während andere kleiner oder größer werden. Ebenfalls gibt es Formen, die spitzer oder flacher werden, je nachdem wie sie verformt werden.
252Triangles
„252 Triangles“ is a project that deals with the manipulation and transformation of a consistently sized circle and its eighths in the form of triangles. The project was inspired by a closer examination of the unfolding of flowers, revealing that they are typically divided into a circle with evenly spaced sections, such as thirds, quarters, sixths, or eighths.
The form study of „252 Triangles“ documents the transformation of a consistently sized eighth of a circle into six different shapes. A circle with a diameter of 27cm is divided into eight equal triangles, and each eighth is deformed into a different shape. The goal of the project was to explore the various three-dimensional forms that can be created from the same surface area and how the volume changes as more deformed eighths are added.
Wire was used for easy deformation and foam rubber as the primary material for the project.
During the experiment, where the eighths of the circle were deformed, it was discovered that each three-dimensional form resulting from the manipulation of a specific triangle has a different volume. Some of the deformed circles close or open, while others become smaller or larger. There are also shapes that become sharper or flatter, depending on how they are deformed.